Trilogía para calcular la sucesión de Fibonacci
- Cálculo iterativo de Fibonacci
- Cómo calcular números Fibonacci con VBA
- Calculando números grandes Fibonacci. Artículo dividido en 2 fragmentos:
Este es el segundo fragmento del tercer artículo sobre números Fibonacci, donde explicaré cómo he diseñado la calculadora de números grandes Fibonacci, que ningún tipo de datos de Excel o de VBA puede soportar.
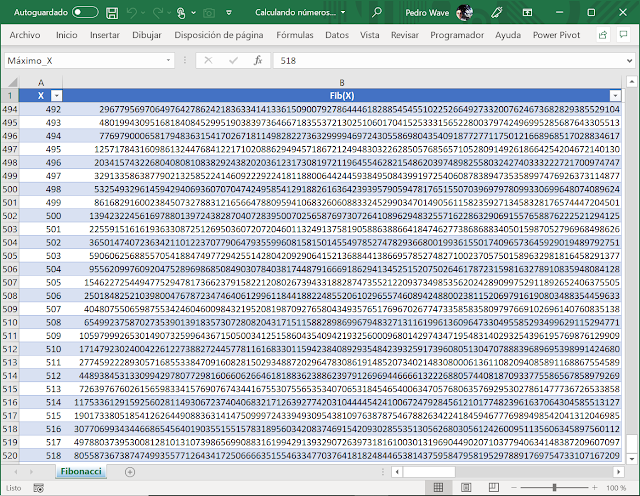
En esta imagen se muestra el Fib(4902) de 1025 cifras, calculado con 114 fragmentos de 9 cifras cada uno. También informa de los tiempos de cálculo, de transformación en texto y de carga en la hoja.
Leyendo este artículo sabrás responder a estas preguntas:
0️⃣0️⃣ Cómo declarar variables
0️⃣1️⃣ Cómo borrar datos de salida
0️⃣2️⃣ Cómo validar datos de entrada
0️⃣3️⃣ Cómo calcular números grandes
0️⃣4️⃣ Cómo establecer límites al cálculo
0️⃣5️⃣ Cómo conocer el progreso del cálculo
0️⃣6️⃣ Cómo detener, continuar o abortar el cálculo
0️⃣7️⃣ Cómo medir tiempos de cálculo
0️⃣8️⃣ Cómo copiar datos en rangos de celdas
0️⃣9️⃣ Cómo visualizar números grandes
1️⃣0️⃣ Cómo imprimir datos de salida
1️⃣1️⃣ Cómo proteger datos de salida
1️⃣2️⃣ Cómo guardar datos de salida
Números grandes (Big numbers)
Esta calculadora se basa en fragmentar o trocear los números grandes en números pequeños de 9 cifras, sumar los números de 9 cifras, acarrear el desbordamiento de la décima cifra al número fragmentado superior, y así sucesivamente hasta completar el total de cifras del número grande.
Se verá mejor con un ejemplo de cálculo de números Fibonacci:
El número mas grande que admite el tipo Decimal en VBA es de 29 cifras:
- 79228162514264337593543950335 = Límite mayor del tipo Decimal.
El mayor número Fibonacci que admite el tipo Decimal es el siguiente, de 29 cifras:
- 50095301248058391139327916261 = Fib(139)
El siguiente número Fibonacci también tiene 29 cifras pero es mayor que el límite del tipo Decimal:
- 81055900096023504197206408605 = Fib(140)
Por lo que el Fib(140) no cabe en un número del tipo Decimal y menos caben los de más de 29 cifras.
El problema es que no se puede usar el tipo Decimal para sumar números Fibonacci de más de 29 cifras como el siguiente, que es de 30 cifras:
- 131151201344081895336534324866 = Fib(141)
¿Cómo podemos sumar números de más de 29 cifras?
La solución es fragmentar los números grandes en un tipo de datos con el que se pueda sumar.
He elegido el tipo Long cuyo límite superior es: 2147483647, usando sólo 9 cifras, y la décima cifra se usa para acarrear el desbordamiento de la suma de las 9 cifras.
Veamos la suma de 4 fragmentos de 9 cifras, que permiten sumar números de hasta 36 cifras.
Primero se suman las 9 cifras del fragmento 1, luego las 9 cifras del fragmento 2 añadiendo un 1 si la suma de los fragmentos 1 llegaba a la décima cifra, y así sucesivamente hasta completar la suma de los 4 fragmentos:
4 3 2 1 = Fragmentos de 9 cifras sumados independientemente
000000050 095301248 058391139 327916261 = Fib(139) de 29 cifras en tipo Decimal.
000000081 055900096 023504197 206408605 = Fib(140) de 29 cifras > tipo Decimal.
000000131 151201344 081895336 534324866 = Fib(141) = Fib(140) + Fib(139) de 30 cifras.
La numeración de fragmentos siempre se hace de derecha a izquierda. En cada uno de los 4 fragmentos se han añadido ceros por la izquierda hasta completar sus 9 cifras.
Este caso es muy simple, pues ninguno de los 4 fragmentos de 9 cifras produce acarreo de la décima cifra.
En cuantos más fragmentos se divida un número, mayores serán los números que se puedan sumar para calcular la sucesión de Fibonacci. Esta calculadora permite dividir un número grande en hasta 3641 fragmentos, con los que se puede llegar a calcular el Fib(156790) de 32767 cifras.
Si quieres profundizar sobre el cálculo con números grandes (big numbers), lee este artículo en inglés:
Descarga la calculadora de Fibonacci
Para seguir las explicaciones es mejor descargar el archivo de ejemplo, con la hoja protegida sin contraseña, desde cualquiera de estos enlaces:
- Microsoft OneDrive: Calculando números grandes Fibonacci - PW1.xlsm
- Sites Google Drive: Calculando números grandes Fibonacci - PW1.xlsm
Abre el archivo y habilita la edición y las macros para poder hacer los cálculos y comprender su diseño funcional.
Abre el Editor VBA con la combinación de teclas: Alt + F11
Funciona escribiendo el número de Fibonacci a calcular en la celda E1 y haciendo clic en la imagen con la espiral de Fibonacci. Hacer clic en la papelera para borrar los números.
Diseño de la calculadora de Fibonacci
La calculadora de números grandes de Fibonacci está diseñada en lenguaje VBA, dentro del módulo MóduloFibonacci, con las siguientes macros:
- CalcularFibonacci: Ejecuta al hacer clic en la foto con la espiral de Fibonacci.
- CalculaSucesiónFibonacci: Calcula la sucesión de Fibonacci hasta un número máximo.
- TransformarFibonacci: Transforma los números Fibonacci en texto.
- CargarFibonacci: Carga los textos Fibonacci en un rango de celdas.
- GuardarTiempos: Guarda los tiempos de cálculo, transformación y carga en un mensaje.
- BorrarFibonacci: Borra el resultado anterior.
- ProtegerHojaActiva: Protege o desprotege la hoja activa.
Todas las macros incluyen comentarios de las instrucciones, primero para recordar qué hacen, y luego para que puedan ser modificadas por quien venga detrás.
Esta calculadora de números grandes de Fibonacci incluye las siguientes funcionalidades:
0️⃣0️⃣ Cómo declarar variables
La instrucción Option Explicit se usa a nivel de módulo para forzar la declaración explícita de todas las variables de ese módulo.
La constante CTE_FRAG define el máximo número permitido dentro de un fragmento del tipo Long.
Lista de constantes y variables del módulo:
Las variables empleadas son del tipo Private, al alcance del módulo, con lo que incluso se pueden analizar después de finalizar la ejecución de las macros.
0️⃣1️⃣ Cómo borrar datos de salida

Antes de hacer cualquier cálculo, limpia automáticamente los datos anteriores de salida, para que no interfieran con los nuevos datos. También se pueden borrar manualmente los datos haciendo clic en la papelera.
0️⃣2️⃣ Cómo validar datos de entrada
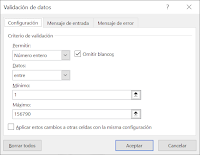
En la celda E1 se valida el número máximo X para el que se calculará la sucesión de Fibonacci, siendo un entero entre 1 y 156790, debido al límite máximo de 32767 cifras guardadas como texto en una celda.
Parte de la macro CalcularFibonacci:
0️⃣3️⃣ Cómo calcular números grandes

En la celda E1 se introduce el número de Fibonacci a calcular y se hace clic en la espiral de Fibonacci (también se puede ejecutar con el método abreviado del teclado: Control + Mayúsculas + C), que ejecuta esta parte de la macro CalcularFibonacci:
El calculo de la variable iMaxFrag es una estimación, suponiendo que cada 4,78 números Fibonacci se incrementa una cifra su valor.
La división por 9 es debida a que los fragmentos son variables del tipo Long de 9 cifras. Se añade un 1 por seguridad de que cabrán todas las cifras en el número de fragmentos.
Con esta estimación las pruebas han resultado satisfactorias hasta ahora. Si se detectan casos de errores en la segmentación habrá que ajustar ese valor. Quien quiera puede mejorar la fórmula del cálculo del número de fragmentos...
La función CalculaSucesiónFibonacci realiza el cálculo:
El cálculo se hace con una matriz redimensionada como Fib(0 To FibMax, 1 To iMaxFrag) con datos del tipo Long con los números Fibonacci siendo guardados como fragmentos de 9 cifras significativas.
La primera dimensión es para los números de Fibonacci desde el 0 al máximo a calcular (FibMax). La segunda dimensión es para los fragmentos de números del tipo Long de 9 cifras significativas.
Las variables del tipo Long son enteros largos, siendo su mayor valor positivo: 2.147.483.647, por lo que la décima cifra por la izquierda sólo puede valer 0, 1 y 2, y para el caso de 2 el resto de cifras no forman un número completo de 9 cifras, por lo que hay que prescindir de números iguales o mayores que 2.000.000.000 en los cálculos fragmentados.
El cálculo con números del tipo Long se limitará hasta el valor 1.999.999.999 pero únicamente se almacenarán números de 9 cifras, del 0 al 999.999.999, siendo la cifra de la izquierda usada para saber si hay desbordamiento en la suma de los dos fragmentos de los anteriores números Fibonacci.

Como ejemplo vamos a calcular el primer número Fibonacci que necesita 2 fragmentos de 9 cifras, que es el Fib(45).
Abriendo en el Editor VBA la Ventana Locales, los dos números anteriores son Fib(43) y Fib(44), que son de 9 cifras, por lo que caben en un tipo Long delimitado a 9 cifras. Pero su suma hace que Fib(45) sea de 10 cifras, por lo que no cabe en un tipo Long delimitado a 9 cifras.
El cálculo del número Fib(45) se hace así:
- Se suman los fragmentos de orden inferior (es la segunda dimensión de la matriz): Fib(43,1) + Fib(44,1) resultando un número de 10 cifras.
- Se guardan las 9 cifras de la derecha del resultado de la suma en el primer fragmento Fib(45,1)
- Se guarda el valor 1 de la décima cifra en la variable de desbordamiento (iDesb) para poder sumarlo al segundo fragmento Fib(45,2).
- Se repite este proceso para los fragmentos de orden superior.
Cuando la suma de dos fragmentos de 9 cifras sobrepasa las 9 cifras, se produce desbordamiento que hay que acarrearlo en la suma de fragmentos de orden superior.
¡Este es el truco usado para poder sumar números Fibonacci de muchas cifras!
Mi modesta tableta, con Windows 10 y con 2 GB de RAM, calcula en menos de 8 minutos hasta el Fib(151660) de 31695 cifras con 3522 fragmentos de 9 cifras. Números de Fibonacci más grandes generan errores de memoria en mi tableta.
¿Cuál es el mayor número Fibonacci que puede calcular tu máquina?
0️⃣4️⃣ Cómo establecer límites al cálculo
Los límites en el cálculo son debidos a la imposibilidad de guardar infinitas cifras en una celda con formato Texto.
En el apartado 0️⃣2️⃣ Cómo validar datos de entrada ya se ha establecido el número Fib(156790) como el número máximo de cálculo de la sucesión de Fibonacci, debido al límite máximo de 32767 cifras guardadas como texto en una celda.
El proceso de guardar los números Fibonacci, fragmentados en números del tipo Long de 9 cifras, en variables del tipo Texto, lo hace la macro: TransformarFibonacci
El número Fib(4901) contiene 1024 cifras, que es el máximo número de caracteres visualizados en una celda. Hasta ese número se visualizan todos los números del Fib(0) al Fibonacci calculado.
A partir del Fib(4902) solamente se visualiza el último número Fibonacci calculado.

Dos bucles recorren la matriz Fib(), con los números fragmentados, para construir la matriz sFib(1 To lFib - lNum, 1 To 2) del tipo String.
La primera dimensión son los valores X guardados como texto, por ejemplo X=45 se guarda en sFib(46,1) y Fib(45) se guarda en sFib(46,2) que es la segunda dimensión de la matriz.
Con la función String() se añaden ceros "0" por la izquierda hasta completar las 9 cifras de cada fragmento del número del tipo Long.
0️⃣5️⃣ Cómo conocer el progreso del cálculo
En la barra de estado se informa, cada 1000 sumas, tanto del progreso del cálculo como de la transformación de los números fragmentados en texto.
0️⃣6️⃣ Cómo detener, continuar o abortar el cálculo

El cálculo arranca al hacer clic en la imagen con la espiral de Fibonacci. Si se hace clic de nuevo en esa imagen, se para el cálculo y se pregunta:
¿Seguir calculando?
Respondiendo No, continua el cálculo.
Respondiendo Sí, se aborta el cálculo y se informa con el mensaje de la izquierda que no se ha conseguido obtener el número Fibonacci buscado, sino un número inferior debido a abortar el cálculo.
Para ejecutar otros eventos del sistema se ha colocado estratégicamente en las macros la instrucción: DoEvents, que permite volver a lanzar la macro CalcularFibonacci tantas veces como se haga clic en la imagen con la espiral de Fibonacci:
0️⃣7️⃣ Cómo medir tiempos de cálculo

Durante el proceso de cálculo se guarda el Timer al inicio del proceso. Al finalizar el proceso, con un mensaje se informan los tiempos de cálculo, de transformación de los fragmentos de números en texto y de carga de los números en formato texto en las celdas de la hoja.
El ejemplo es para el Fib(99999) que ha sido calculado en unos 214 segundos, menos de 4 minutos en mi tableta.
¡Seguro que en tu máquina cuesta menos calcularlo que en la mía!
La macro que va montando el mensaje final con los tiempos es la siguiente:
0️⃣8️⃣ Cómo copiar datos en rangos de celdas
Habiendo declarado una matriz del tipo Texto con la instrucción:
Private sFib() As String
Y redimensionada como matriz de dos dimensiones, siendo la primera dimensión el número de Fibonacci calculados y con la segunda dimensión se guarda X y Fib(X):
ReDim sFib(1 To lFib, 1 To 2) As String
Prácticamente una única instrucción copia los números, convertidos en texto dentro de la matriz sFib, y los pega en las celdas de las columnas A (valor de X) y B (valor de Fib(X)):
Range("A2:B" & lFila) = sFib
Siendo lFila el número de fila que corresponde al último número de Fibonacci a pegar en el rango de celdas y sFib la matriz del tipo String con los números convertidos en texto.
Igualar un rango de una hoja de cálculo con una matriz VBA de dos dimensiones es muchísimo más rápido que hacer lo mismo con un bucle que recorra la matriz para copiar sus valores y pegarlos individualmente en cada celda. Microsoft no lo explica bien en este enlace: Uso de matrices (VBA) | Microsoft Docs. En este enlace está mejor explicado: Arrays And Ranges In VBA (cpearson.com)
La macro CargarFibonacci realiza todo el proceso, creando una tabla con los valores en formato texto de X y Fib(X), siendo la principal instrucción la que iguala el rango con la matriz sFib:
0️⃣9️⃣ Cómo visualizar números grandes
Microsoft dice que el límite de caracteres visualizados en una celda es de 1024, aunque en la celda se puedan guardar textos de hasta 32767 caracteres.
Al ajustar el texto en las celdas he comprobado que, con el ancho de columna establecido, se puede visualizar hasta el Fib(14605) de 3052 cifras. Se pueden visualizar números mayores si se aumenta el ancho de la columna B.
Se pueden visualizar números más grandes en la barra de fórmulas:
En cualquier caso, siempre se pueden copiar las celdas y pegarlas en el bloc de notas.
1️⃣0️⃣ Cómo imprimir datos de salida
Para imprimir desde el menú: Archivo > Imprimir, con lo que se abre la presentación previa de las páginas a imprimir:
Cuando se calculan números mayores que Fib(4901), sólo se puede imprimir un único número Fibonacci y la impresión será parcial para números con muchas cifras, como se ha comentado en el apartado anterior explicando cómo visualizar números grandes.
1️⃣1️⃣ Cómo proteger datos de salida
La macro para proteger los datos de salida es ProtegerHojaActiva:
La protección permite modificar únicamente la celda E1 con el número máximo de Fibonacci a calcular.
No se puede crear una tabla o borrar un rango dentro de una hoja protegida, por lo que en esos casos se debe quitar la protección de la hoja previamente.
1️⃣2️⃣ Cómo guardar datos de salida
Antes de guardar la plantilla se debe decidir si se quieren guardar los números de Fibonacci calculados.
Si no se quieren guardar se debe hacer clic en la imagen de la papelera para borrar la tabla de datos antes de guardar el archivo.
Para guardar se hace clic en el icono con el diskette 💾 o desde el menú: Archivo > Guardar o Guardar como
Conclusiones
Este artículo debe servir de ejemplo de técnicas y algoritmos de cálculo de números grandes, aunque lo fundamental es que el cálculo con números grandes no se debe hacer en VBA y/o en Excel. Es más conveniente usar librerías específicas de números grandes, por ejemplo en el lenguaje R con la clase bigz: Large Sized Integer Values.
Importa mucho elegir qué tipo de dato va a ser el menor fragmento de un número grande. En este ejemplo se ha elegido el tipo Long. En el artículo anterior se comentó que para otros algoritmos se había elegido el tipo String o el tipo Byte. Sería interesante probar con otros tipos de datos VBA, como Int, Double e incluso Decimal, para saber si mejora la eficacia del algoritmo y bajan los tiempos de cálculo.
Pero eso se lo dejo como ejercicio a los lectores de este modesto blog de Excel...